현재 중등교육 과정에 유리화하는 방법이 나온다.원리는 간단하다. 분모에 제곱근이 있는 것을 분모 분자에 적당한 기작을 해줘서 분모에 제곱근을 없애주는 것이다.
그냥 간단히 하나일때는 그 수를 분모 분자에 곱하면 제곱되서 사라진다.
결합이 안되는 두개의 제곱근이 있다했을때는
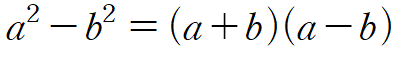
를 이용하여 두 수 모두 동시에 제곱되게 해준다. 정말 곱셈공식의 힘은 대단한것 같다. 결합안되는 무리수를 한방에 동시에 없앤다는게 처음에는 하나도 안 신기했는데, 이것이 이 연구의 영감이 되게 해줬다.
tmi를 잠시 말하면 난 중학교 수학시간이 너무 심심해서 수업만 들으면 시간이 낭비되는거 같아 선생님과 교과서의 모든 것 심지어 공리까지 의심을 품고 새로운걸 생각하려 했다. 그리고 이걸 배웠을때도 왜 굳이 2개만 하지? 하고서 바로 분모에 여래개의 제곱근이 더하거나 빼기로 연결됐을때 유리화 하는 법을 찾아내고 말것이다 다짐했다.
곱셈 공식에서 보면 쉽게 알 수 있듯이 우리의 목적은 a+b 만있는 식에 여러 항을 곱해 차수가 짝수가 되게끔 하는것이다.
이러면 기본 아이디어는 끝났다.
막상 시작하려니 이 기본아이디어는 수학적 해결을 가져다 주진 못했다. 그래서 일단 3개인 경우를 해보고 다시 관찰해보기로 했다.
이건 그냥 위에 했던 방식에다 좀 추가된건데 두개를 하나로 묶어서 ((a+b)+c)((a+b)-c)로 하면 루트ab 항만 남는데, 이건 다시 똑같이 위에서 한거로 하면 된다. 이제 이걸 내 아이디어로 표현해보면
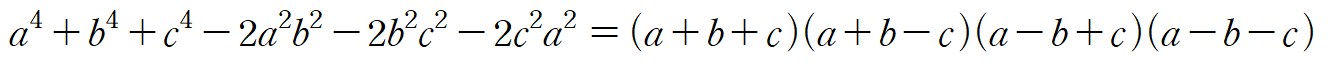
우와 정말 짝수차만 남는것을 볼 수 있었다.
이제 4개인 경우도 똑같이 할 수 있겠지? 2개,2개로 나눠서 할 수 있다.
하지만 5개가 되는순간 1,4로 나눠서 합차공식을 쓰면 오히려 제곱근 항은 늘어나고 2,3으로 나눠도 항은 그대로 5개가 나온다.
흠...솔직히 뭐 계속 하다보면 제곱근이 사라질 수도 있지 않나 생각들었지만 이걸 5개여도 하기가 망설여 지는데 그 이후는 너무 항이 많아 검증하기 힘드니까 포기하고 다른 방법을 찾았다.
여기서 내 수학적 직관력을 발휘했다. 2와 3인경우 첫항을 제외하고 모두가 +,-인 경우를 곱한 것이라 해석했다. 이 가설로 4개인 경우를 노가다로 구하니까(각각이 4개가 결합된 2^3개의 괄호항)거짓말처럼 짝수차만 나왔다.
그 당시 내 직관력만 믿고 나머지는 일반화해서 된다는걸 증명안하고 이게 맏는다고 굳게 믿고 살았었다. 그리고 반 친구들한테 묶어서 푸는 방법은 안되는 1/(sqrt(2)+sqrt(3)+sqrt(5)+sqrt(7)+sqrt(11))을 유리화 하시오 이런 문제도 막 냈는데 역시 4개 까지는 하던 놈들이 이건 못했고, 난 당당히 2^4 즉 16개의 괄호 항만 곱하면 된다만 하고 말았다. 그리고 2년이 지난 시점 갑자기 이 증명 못한 문제가 떠올랐고 마침 시험기간이라 할것도 없겠다(?) 증명해보기로 하고 8분만에 증명을 끝냈다ㅋㅋㅋㅋ

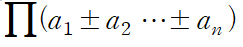
맨 앞 항 제외 나머지 항들이 모두 +,- 한번씩 있는 경우를 다음과 같이 나타내었다. 이제 임의의 ai항이 짝수차항만 존재함을 보이면 된다. 이미지에서 볼 수 있듯, 어떤 +,-조합을 가진 괄호항은, ai의 부호만 바꾸고 나머지 부호는 그대로인 조합을 가진 괄호항이 무조건 존재하기 때문에 이 둘씩 곱하면 Aj에 ai가 포함안되고 ai만 따로 제곱항만 있는것을 볼 수 있다. 여기서 전개해도 ai는 짝수차 끼리의 합이 될테니 어쨋든 짝수차 이므로 증명이 완료된다.
다시 한번 유리화 모습에 대해 정리를 하자면
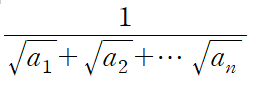
을 유리화 하는방법은
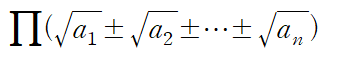
을 분모 분자에 곱해주면 된다.
(괄호항만 무려 2^(n-1)개)
아 참고로 n=3일때 식이 헤론 공식과 같다.
이후에 세제곱근 항같은것도 일반화 하려 시도했는데 그건 실패했고 lemma로써
분모에 2의 거듭제곱근 꼴만 존재하면(ex,네제곱근, 16제곱근) 유리화 가능이다.
증명은 그냥 1번 이 시행을 하면 적어도 제곱이 되는데 또 한번 더하면 이제 네제곱근은 사라질것이고, 계속하면 2의 거듭제곱근 꼴이 다 사라지게 된다.

이건 조금 더 설명이 추가된 최초 즉석 필기 버전이다.
오늘 이렇게 2년 동안 묵혀온 유리화 일반화 증명을 해냈고, 추가로 lemma까지 만들어보았다. 이를 이어 '유리화 가능'의 범위를 확장 시키는 사람이 나왔으면 좋겠다.