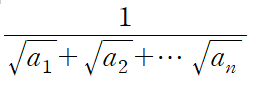tosemary 님의 블로그

현재 중등교육 과정에 유리화하는 방법이 나온다.원리는 간단하다. 분모에 제곱근이 있는 것을 분모 분자에 적당한 기작을 해줘서 분모에 제곱근을 없애주는 것이다. 그냥 간단히 하나일때는 그 수를 분모 분자에 곱하면 제곱되서 사라진다. 결합이 안되는 두개의 제곱근이 있다했을때는 를 이용하여 두 수 모두 동시에 제곱되게 해준다. 정말 곱셈공식의 힘은 대단한것 같다. 결합안되는 무리수를 한방에 동시에 없앤다는게 처음에는 하나도 안 신기했는데, 이것이 이 연구의 영감이 되게 해줬다. tmi를 잠시 말하면 난 중학교 수학시간이 너무 심심해서 수업만 들으면 시간이 낭비되는거 같아 선생님과 교과서의 모든 것 심지어 공리까지 의심을 품고 새로운걸 생각하려 했다. 그리고 이걸 배웠을때도 왜 굳이 2개만 하지? 하고서 바로 ..

보통 도플러는 1차원 운동만 고려한다. 특수한 경우라 하면은 이 1차원 운동을 제외한 모든 경우를 뜻한다. 문제:듣는이는 v로 움직이고 음향과의 거리는 L이다.(최단 거리) 이때 듣는이의 진동수는 어떤 그래프를 나타낼까   일단 t=0일때를 최단거리일때로 가정하면 이런식으로 나오고, 개형은 다음과 같다. 이 경우 L=1m이고 움직이는 속도가 음속의 2/3 일때를 나타내서 거의 원래 소리의 2배, 혹은 1/2배까지 낮은 소리까지 들을 수 있다.

카탈란수 하면 2xn 블록을 차례대로 쌓는거랑 동치다. 이해를 쉽게 틀을 45도 정도로 회전하고 중력의 영향에 의해 블록을 쌓는다 생각하면 된다. 또한 다른 예시로 n*n을 조건에 맞게 이동하는 것과 같다.(위아니면 오른쪽인데 위로 가는건 총 오른쪽으로 간 횟수보다 많으면 안된다.)여기까지는 수학에 관심이 깊은 사람이면 알만하다. 근데 대부분 그 이상을 모를 것이다. n*n*n을 x,y,z로 이동 가능한데, 총이동 거리가 x>=y>=z가 되게 이동하는 경우의 수라 확장하고, 3차원 카탈란수라 이름 지을 수 있다. 사실 카탈란수는 이런 기하적인 예시와 전혀 관련이 없고 이항계수에서 유래되었기에 3차원 카탈란수라 이름 짓기에는 오류가 생기는데 팩트가 사람들은 아마 이런 기하적 예시로 카탈란 수를 기억하기 때..

import sysimport itertoolsimport numpy as npfrom math import combdef compute_max_region_count(k, n, vectors):    # 1. 초기 영역분할 최대 수 p 계산    p = sum(comb(n, i) for i in range(k + 1))  # p = nC0 + nC1 + ... + nCk    # 2. 조합을 이용하여 벡터 선택 및 랭크 검사    for r in range(2, k + 1):  # 2개부터 k개까지 선택        for subset in itertools.combinations(vectors, r):            matrix = np.array(subset)            if np.l..